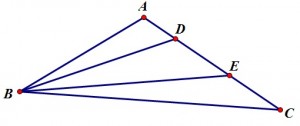
[Toán lớp 7] Cho tam giác ABC, góc A là góc tù. Trên cạnh AC lấy hai điểm D và E (D nằm giữa A và E). Chứng minh rằng BA < BD < BE < BC.
Giải
Trong có góc BAD tù nên góc BAD > góc ADB => BD > BA. (1)
Ta có góc BDE = góc BAD + góc ABD (vì …)
Suy ra góc BDE là góc tù, vậy góc BDE là góc lớn nhất trong 3 góc của tam giác BDE.
Trong tam giác BDE ta có: góc BDE > gocsBED => BE > BD. (2)
Tương tự có góc BEC tù, trong tam giác BEC có góc BEC > góc BCE => BC > BE (3)
Từ 1, 2 và 3 suy ra: BA < BD < BE < BC (dpcm)








Chung minh goc tu vi sao ah?
hay qá
Đề thi môn toán trường mấy bn có chưa gửi biện pháp nhanh cho mk ik